Binomio al cuadrado(reducción de ecuaciones).

Resolución de sistemas de ecuaciones por el método de reducción

1. Se preparan las dos ecuaciones, multiplicándolas por los números que convenga.

2. La restamos, y desaparece una de las incógnitas.

3. Se resuelve la ecuación resultante.

4. El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve.

5. Los dos valores obtenidos constituyen la solución del sistema.

ejemplo: 

Lo más fácil es suprimir la y, de este modo no tendríamos que preparar las ecuaciones; pero vamos a optar por suprimir la x, para que veamos mejor el proceso.

Restamos y resolvemos la ecuación:

Sustituimos el valor de y en la segunda ecuación inicial.

Solución:

Binomio de suma al cuadrado

Un binomio al cuadrado (suma) es igual es igual al cuadrado del primer término, más el doble producto del primero por el segundo más el cuadrado segundo.

(a + b)² = a² + 2 · a · b + b²

(x + 3)² = x ² + 2 · x ·3 + 3 ² = x ² + 6 x + 9

Binomio de resta al cuadrado

Un binomio al cuadrado (resta) es igual es igual al cuadrado del primer término, menos el doble producto del primero por el segundo, más el cuadrado segundo.

(a − b)² = a² − 2 · a · b + b²

(2x − 3)² = (2x)² − 2 · 2x · 3 + 3 ² = 4x² − 12 x + 9

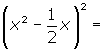
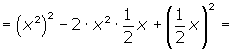
El desarrollo de un un binomio al cuadrado se llama trinomio cuadrado perfecto.

a² + 2 a b + b² = (a + b)²

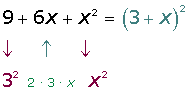
a² − 2 a b + b² = (a − b)²

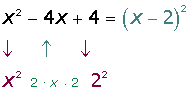
Aqui esta un power point sobre el tema:

http://www.slideshare.net/maruja1945/sistema-de-ecuaciones-metodo-de-reduccin-13487462#btnNext

Un video de este tema:).

http://www.youtube.com/watch?v=o1wIYfvHzCc

http://www.youtube.com/watch?v=Fa7mpIpRVE4

http://www.youtube.com/watch?v=1-MKDIwP9t8

pues entendí que un binomio consta únicamente de dos términos, separados por un signo de más (+) o de menos (-). En otras palabras, es un polinomio formado por la suma de dos monomios